1. Proporsisi Bersyarat (Implikasi)

Selain dalam bentuk konjungsi, disjungsi, dan negasi, proposisi majemuk juga dapat muncul berbentuk “jika p, maka q”, seperti contoh-contoh berikut :

1. Jika adik lulus ujian, maka ia mendapat hadiah dari ayah.
2. Jika suhu mencapai 80°C, maka alarm berbunyi.
3. Jika anda tidak mendaftar ulang, maka anda dianggap menggundurkan diri.

Pernyataan berbentuk “jika p, maka q” semacam itu disebut proporsisi bersyarat atau kondisional atau implikasi.

DEFINISI 1.6. Misalkan p dan q adalah proposisi. Proposisi majemuk “jika p, maka q” disebut proposisi bersyarat (implikasi dan dilambangkan dengan :

p→q

Proposisi p disebut hipotesisi (atau antesenden atau premis atau konddidi) dan proposisi q disebut konklusi ( konsekuen).

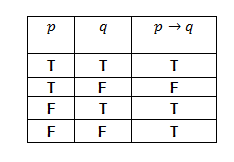
Tabel kebeneran implikasi ditunjukan pada tabel 1.8

Catatan : impilasi p→q, hanya salah jika p benar tetapi q salah, selain itu implikasi bernilai benar.Hal ini dijelaskan dengan contoh analogi berikut : Misalkan dosen anda berkata kepada mahasiswanya di dalam kelas “ jika nilai ujian anda 80 atau lebih, maka anada akan mendapat nilai A untuk kuliah ini” apakah dosen anda mengatakan kebenaran atau dia berbohong ? tinjau empat kasus berikut ini :

Kasus 1 : Nilai ujian akhir anda diatas 80 (hipotesis benar) dan anda mendapat nilai A untuk mata kuliah tersebut (konklusi benar). Pada kasus ini, pernyataan dosen anda benar.

Kasus 2 : Nilai ujian akhir anda diatas 80 (hipotesis benar) tetapi anda tidak mendapat nilai A (konklusi salah). Pada kasus ini, dosen anda berbohong (pernyataan salah).

Kasus 3 : Nilai ujian akhir anda dibawah 80 (hipotesis salah) dan anda mendapat nilai A (konklusi benar). Pada kasus ini, dosen anda tidak dapat dikatakan salah (mungkin ia melihat kemampuan anda secara rata-rata bagus sehingga ia tidak ragu memberi nilai A).

Kasus 4 : Nilai ujian akhir anda di bawah 80 (hipotesis salah) dan anda tidak mendapat nilai A (konklusi salah). Pada kasus ini, dosen anada benar.

Di dalam bahasa alami (bahasa percakapan manusia), seperti Bahasa Indonesia dan Bahasa Inggris, terdapat hubungan sebab-akibat antara hipotesisi dengan konklusi, misalnya pada implikasi.

“Jika suhu mencapai 80°C, maka alarm berbunyi.”

Implikasi seperti ini adalah normal dalam Bahasa Indonesia. Tetapi, dalam penalaran matematik, kita memandang implikasi lebih umumm daripada implikasi dalam bahasa alami. Konsep matematik mengenai implikasi independen dari hubungan sebab-akibat antara hipotesis dan konklusi. Definisi kita mengenaiimplikasi adalah pada nilai kebenarannya, bukan didasarkan pada penggunaan bahasa [ROS03]. Misalnya pada implikasi

“Jika Paris adalah ibukota Perancis, maka 1+1=2”

Implikasi di atas tetap valid secara matematis meskipun tidak ada kaitan anatara Paris sebagai ibukota Perancis dengan 1+1=2. Implikasi tersebut bernilai benar karena hipotesis benar (Paris ibukota Perancis adalah benar) dan konklusi jga benar (1+1=2 adalah benar). Implikasi :

“Jika Paris adalah ibukota Perancis, maka 1+1=3”

Bernilai salah karena hipotesis benar tetapi 1+1=3 salah.

Implikasi p→q memainkan peran penting dalam penalaran. Implikasi ini tidak hanya diekspresikan dalam pernyataan standard “ jika p, maka q” tetapi juga dapat diekspresikan dalam berbagai cara, antara lain :

1. Jika p, maka q (if p, then q)
2. jika p, q (if p, q )
3. p mengakibatkan q (p implies q)
4. q jika p (q if p )
5. p hanya jika q ( p only if q)
6. p syarat cukup agar q (p isi sufficient for q)
7. q syarat perlu bagi p (q is necessary for p)
8. q bilamana p (q whenever p)

contoh-contoh berikut memprelihatkan implikasi dalam berbagai ekspresi serta bagaimana mengubah berbagai bentuk implikasi menjadi bentuk stabdar “jika p, maka q”.

Contoh 1.12

Proposisi-proposisi berikut adalah implikasi dalam berbagai bentuk :

1. Jika hari ini hujan, maka tanaman akan tumbuh subur.
2. Jika tekanan gas diperbesar, mobil melaju kencang.
3. Es yang mencair di kutub mengakibatkan permukaanair laut naik.
4. Orang itu mau berangkat jika ia diberi ongkos jalan.
5. Ahmad bisa mengambil matakuliah Teori Bahasa Formal hanya jika ia sudah lulus matakuliah Matematika Diskrit.
6. Syarat cukup agar pom bensin meledak adalah percikan api danri rokok.
7. Syarat perlu bagi Indonesia agar ikut Piala Dunia adalah dengan mengontrak pemain asing kenamaan.
8. Banjir bandang terjadi bilamana hutan ditebangi.

Contoh 1.13

Ubahlah proposisi c sampai h di dalam contoh 1.12 ke dalam bentuk proposisi “jika p, maka q”.

Penyelesaian :

1. Jika es yang mencair di kutub, maka permukaanair laut naik.
2. Jika orang itu diberi ongkos jalan, maka ia mau berangkat.
3. Jika Ahmad bisa mengambil matakuliah Teori Bahasa Formal, maka ia sudah lulus matakuliah Matematika Diskrit.
4. Pernyataan yang diberikan ekivalen dengan “percikan api dari rokok adalah syarat cukup untuk membuat pom bensin meledak” atau “ Jika api memercik dari rokok maka pom bensin akan meledak”.
5. Pernyataan yang diberikan ekivalen dengan “mengontrak pemain asing kenamaan adalah syarat perlu untuk Indonesia agar ikut Piala Dunia” atau “Jika Indonesia ikut Piala Dunia maka Indonesia mengontrak pemain asing kenamaan”.
6. Jika hutan-hutan ditebangi, maka Banjir bandang terjadi.

Contoh 1.14

Misalkan :

x : Anda berusia 17 tahun

y : Anda dapat memperoleh SIM

Nyatakan preposisi berikut ke dalam notasi implikasi :

1. Hanya jika anda berusia 17 tahun maka anda dapat memperoleh SIM.
2. Syarat cukup agar anda dapat memperoleh SIM adalah anda berusis 17 tahun.
3. Syarat perlu agar anda dapat memperoleh SIM adalah anda berusis 17 tahun.
4. Jika anda tidak dapat meperoleh SIM maka anda tidak berusia 17 tahun.
5. Anda tidak dapat memperoleh SIM bilamana anda belum berusia 17 tahun.

Penyelesaian :

1. Pernyataan yang memberikan ekivalen dengan “Anda dapat memperoleh SIM hanya jika anda berusia 17 tahun”. Ingat bahwa p→q bisa dibaca “p hanya jika q’. Jadi, pernyataan yang diberikan dilambangkan dengan y→x.
2. Pernyataan yang diberikan ekivalen dengan “Anda berusia 17 tahun adalah syarat cukup untuk dapat memperoleh SIM”. Ingat kembali bahwa p→q bisa dibaca “p syarat cukup untuk q”. Jadi, pernyataan yang diberikan dilambangkan dengan x→y.
3. Pernyataan yang diberikan ekivalen dengan “Anda berusia 17 tahun adalah syarat perlu untuk dapat memperoleh SIM”. Ingat kembali bahwa p→q bisa dibaca “q syarat perlu untuk q”. Jasi, pernyataan yang diberikan dilambangkan dengan y→x.
4. ~y→~x.
5. Ingat kembali bahwa p→q bisa dibaca “q bilamana p”. Jasi, pernyataan yang diberikan dilambangkan dengan ~x→~y.

Contoh 1.15

Tunjukkan bahwa p→q ekivalen secara logika dengan ~p q.

Penyelesaian :

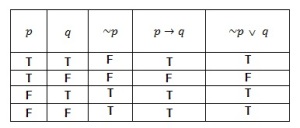
Tabel 1.9 memperlihatkan bahwa memang benar p→q~p  v q. Dengan kata lain pernyataan “Jika p, maka q” ekivalen secara logika dengan “ tidak p atau q”.

Tabel 1.9 tabel kebenaran p→q dan ~p v q

Contoh 1.16

Tentukan ingkaran (negasi) dari p→q

Penyelesaian :

Dari contoh 1.15 sudah ditunjukan bahwa p→q ekivalen secara logika dengan ~p q gunakan hukum DeMorgan untuk menentukan ingkaran dari p→q :

~(p→q) ~(~p q)   ~(~p)~q  p~q

 

Contoh 1.17

Dua pedagang barang kelontong mengeluarkan moto jitu untuk menarik pembeli. Pedagang pertama mengumbar moto “Barang bagus tidak murah” sedangkan pedagang kedua mempunyai moto “Barang murah tidak bagus”. Apakah kedua moto tersebut menyatakan hal yang sama ?

Penyelesaian :

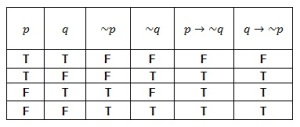
Untuk memeriksa “Apakah kedua moto tersebut sama, kita perlu membandingkan tabel kebenaran keduanya. Misalkan p menyatakan proposisi “Barang itu bagus” sedangkan q menyatakan “Barang itu murah”. Maka moto pedaganf pertama dapat ditulis sebagain “Jika barang itu bagus maka barang itu tidak murah” atau p→~q, sedangkan moto kedua dapat ditulis sebagai “Jika barang itu murah maka barang itu tidak bagus” atau q→~p. Tabel kebenaran untuk proposisis p→~q dan proposisi q→~p sama, dengan kata lain p→~q q→~p. Jadi kita dapat menyimpulkkan bahwa kedua moto tersebut menyatakan hal yang sama.

Tabel 1.10 tabel kebenaran p→~q dan q→~p

Banyak orang yang bingung mengapa bentuk “p hanya jika q” sama dengan “jika p, maka q” untuk menjelas hal-hal ini kita harus mengingat bahwa “p hanya jika q” menyatakan bahwa p tidak dapat benar bila q salah. Dengan kata lain, menyatakan “p hanya jika q” salah jika p benar, tetapi q salah. Bila p salah, q dapat salah satu dari benar atau salah, karena pernyataan tersebut tidak menyatakan apa-apa tentang nilai kebenaran q .

 

Implikasi dalam Bahasa Pemrograman

Struktur if-then yang digunakan pada kebanyakan bahasa pemrograman berbeda dengan implikasi if-then yang digunakan dalam logika. Struktur if-then dalambahasa pemrograman berbentuk

if c then S

yang dalam hal ini c adalah sebuah ekspresi logika yang menyatakan syarat atau kondisi, sedangkan S berupa satu atau lebih pernyataan. Ketika program dieksekusi dan menjumpai pernyataan if –then, S dieksekusi jika c benar, tetapi S tidak dieksekusi jika c salah.

Pernyataan if-then dalam bahasa pemrograman bukan proposisi karena tidak ada korespondensi antara pernyataan tersebut denan operator implikasi (→). Penginterprestasi bahasa pemrograman (disebut interpreter atau compiler) tidak melakukan penilaian kebenaran pernyataan if-then secara logika. Interpreter hanya memeriksa kebenaran kondisi c, jika c benar maka S dieksekusi, sebaliknya jika c salah maka S tidak dieksekusi. Sebagai contoh, perhatikan contoh 1.18 berikut ini.

Contoh 1.18

Misalkan di dalam sebuah program yang ditulis dalam Bahasa Pascal terdapat pernyataan berikut :

if x>y then y :=x+10;

(Simbol := menyatakan operator pengisian nilai, yaitu nilai ekspresi di ruas kanan simbol := diisikan ke dalam peubah di ruas kiri simbol :=). “x>y” adalah ekspresi logika yang nilainya benar atau salah tergantung pada nilai x dan y sedangkan y :=x+10 adalah sebuah pernyataan aritmatika yang akan dieksekusi jika ekspresi logika x>y benar.

Berapa nilai y setelah pelaksana pernyataan-pernyataan if-then di atas jika nilai x dan y sebelum pernyataan tersebut adalah (i)x=2, y=1, dan (ii) x=3, y=5 ?

Penyelesaian

(i)      sebelum pernyataan if-then nilai x=2 dan y=1, maka ekspresi x>y bernilai benar sehingga pernyataan y :=x+10 dilaksanakan, yang mengakibatkan nilai y sekarang menjadi y =2+10=12.

(ii)     sebelum pernyataan if-then nilai x=3 dan y=5, maka ekspresi x>y bernilai salah sehingga pernyataan y :=x+10 tidak dilakukan. Dalam hal ini, nilai y tetap seperti sebelumnya, yaitu 5.

 

2. Varian Proposis Bersyarat

Terdapat bentu implikasi lain yang berkaitan dengan p→q yaitu proposisi sederhana yang merupakan varian dari implikasi. Ketiga varian proposisi bersyarat tersebut adalah konvers, invers, dan kontraposisi dari proposisi asal p→q.

Konvers ( kebalikan)     :   q→p

Invers                            : ~p→~q

Kontaposisi                    : ~q→~p

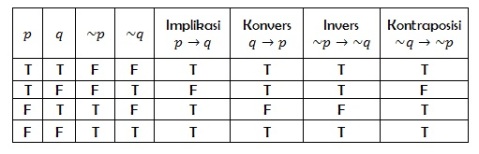
Tabel 1.11 memperlihatkan tabel kebenaran dari ketiga varian proposisi bersyarat tersebut. Dari tabel tersebut terlihat bahwa proposisi bersyarat p→q ekivalen secara logika dengan kontraposisinya, ~q→~p.

Tabel 1.11. tabel kebenaran implikasi, konvers, invers, dan kontraposisi

Contoh 1.19

Tentukan konvers, invers, dan kontraposisi dari pernyataan berikut :

“Jika Amir mempunyai mobil, maka ia orang kaya”

Penyelesaian :

Konvers : Jika Amir orang kaya, maka ia mempunyai mobil.

Invers   : Jika Amir tidak mempunyai mobil, maka ia tidak orang kaya.

Kontraposisi : Jika Amir bukan orang kaya, maka ia tidak mempunyai mobil.

Contoh 1.20

Tentukan kontraposisi dari penyataan :

1. Jika ia bersalah maka ia dimasukkan ke dalam penjara.
2. Jika 6 lebih besar dari 0 maka 6 bukan bilangan negatif.
3. Iwan lulus ujian hanya jika ia belajar.
4. Hanya jika ia tidak terlambat maka ia akan mendapat pekerjaan itu.
5. Perlu ada angin agar layang-layang bisa terbang.
6. Cukup hari hujan agar hari ini dingin.

Penyelesaian :

1. Jika ia tidak dimasukan penjara, maka ia tidak bersalah.
2. Kika 6 bilangan negatif, maka 6 tidak lebih besar dari 0.
3. Pernyataan diberi ekivalen dengan “ jika iwan lulus ujian maka ia sudah belajar”, sehingga kontraposisinya adalah “Jika Iwan tidak belajar, maka ia tidak lulus ujian”.
4. Pernyataan diberi ekivalen dengan “Jika ia mendapat pekerjaan itu maka ia tidak terlambat”, sehingga kontraposisinya adalah “Jika ia terlambat maka ia tidak akan mendapat pekerjaan itu”.
5. Pernyataan yang diberikan dapat ditulis kembali menjadi “Ada angin adalah syarat perlu agar layang-layang bisa terbang” yang dalam hal ini ekivalen dengan “Jika layang-layang bisa terbang maka hari ada angin”. Kontraposisi adalah “Jika hari tidak ada angin, maka layang-layang tidak bisa terbang”.
6. Pernyataan yang diberikan dapat ditulis kembali menjadi “Hari hujan adalah syarat cukup agar hari ini dingin” yang dalam hal ini ekivalen dengan “Jika hari hujan maka hari ini ingin dingin”. Kontraposisinya adalah “Jika hari tidak dingin maka hari tidak hujan”.

3. Bikondisional (Bi-Implikasi)

Proposisi penting lainnya adalah berbentuk “p jika dan hanya jika q” yang dinamakan bikondisional atau bi-implikasi. Definisi bikondisional dikemukakan sebagai berikut.

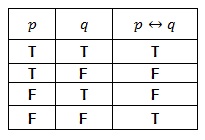
Pernyataan p↔q adalah benar bila p dan q mempunyai nilai kebenaran yang sama, yakni p↔q benar jika p dan q keduannya benar atau p dan q keduannya salah. Tabel kebenaran selengkapnya diperlihatkan pada tabel 1.12

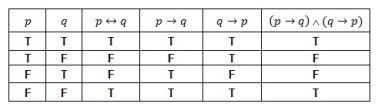
Perhatikan bahwa bikondisionalp↔q ekivalen secara logika dengan (p→q)Λ(q→p). Keekivalenan tersebut ditunjukkan pada tabel 1.13. dengan kata lain, pernyataan “p jika dan hanya jika q” dapat dibaca “Jika p maka q dan jika q maka p”

Tabel 1.13 p↔q ⇔  (p→q)(q→p)

Terdapat sejumlah cara untuk menyatakan bikondisonal p↔q dalam kata-kata, yaitu :

1. p jika dan hanya jika q (p if and only if q)
2. p adalah syarat perlu dan cukup untuk q (p isi necessary and sufficient for q)
3. Jika p maka q, dan sebaliknya (if p then q, and conversely)
4. p iff q

Contoh 1.21

Proposisi majemuk berikut adalah bi-implikasi:

1. 1+1=2 jika dan hanya jika 2+2=4
2. Syarat cukup dan syarat perlu agar hari hujan adalah kelembaban udara tinggi.
3. Jika anda orang kaya maka anda mempunyai banyak uang dan sebaliknya.
4. Bantung terletak di Jawa Barat iff Jawa Barat adalah sebuah profinsi di Indonesia.

Contoh 1.22

Tuliskan setiap proposisi ke dalam bentuk “p jika dan hanya jika q”

1. Jika udara di luar panas maka anda membeli es krim, dan jika anda membeli es krim maka udara di luar panas.
2. Syarat cukup dan perlu agar anda memenangkan pertandingan adalah anda melakukan banyak latihan.
3. Anda naik jabatan jika anda punya koneksi, dan anda punya koneksi jika anda naik jabatan.
4. Jika anda lama menonton telivisi maka mata anda lelah, begitu sebaliknya.
5. Kereta api datang terlambat tepat pada hari-hari ketika saya membutuhkannya.

Penyelesaian :

1. Anda membeli es krim jika dan hanya jika udara di luar panas.
2. Anda melakukan banyak latihan adalah syarat perlu dan cukup untuk anda memenangkan pertandingan.
3. Anda naik jabata jika dan hanya jika anda punya koneksi.
4. Mata anda lelah jika dan hanya jika anda lama menonton televisi.
5. Kereta api datang terlambat jika dan hanya jika saya membutuhkan kereta hari itu.

Contoh 1.23

sebuah pulau didiami oleh dua suku asli. Penduduk suku pertama selalu mengatakan hal yang benar, sedangkan penduduk dari suku lain selalu mengatakan kebohongan. Anda tiba di pulau ini dan bertanya kepada seorang penduduk setempat apakah di pulau tersebut ada emas atau tidak. Ia menjawab, “Ada emas di pulau ini jika dan hanya jika saya selalu mengatakan kebenaran”. Apakah emas di pulau tersebut ?

Penyelesaian :

Misalkan

p :saya selalu menyatakan kebenaran.

q :ada emas di pulau ini.

Pernyataan orang tersebut dapat dinyatakan sebagai :

p↔q

Tinjau dua kemunhkinan kasus mengenai orang yang kita tanya tad. Kasus 1, orang yang memberi jawaban adalah orang dari suku yang selalu menyatakan hal yang benar. Kasus 1, orang yang memberi jawaban adalah orang dari suku yangs selalu menyatakan hal yang bohong. Kita analisis setiap kasus persatu sebagai berikut :

Kasus 1 : Orang tersebut selalu menyatakan hal yang benar. Ini berarti p benar, dan jawaban terhadap pernyataan kita pasti juga benar, sehingga pernyataan bi-implikasi tersebut bernilai benar. Dari tabel 1.12 kita melihat bahwa bila p benar dan p↔q benar, maka q harus benar. Jadi, ada emas di pulau tersebut adalah benar.

Kasus 2 : Orang tersebut selalu menyatakan hal yang bohong. Ini berarti p salah, dan jawaban terhadap pernyataan kita pasti juga salah, sehingga pernyataan bi-implikasi tersebut salah. Dari tabel 1.12 kita melihat bahwa bila p benar dan p↔q salah, maka q harus benar. Jadi, ada emas di pulau tersebut adalah benar.

Dari kedua kasus, kita selalu berhasil menyimpulkan bahwa ada emass di pulau tersebut, meskipun kita tidak dapat memastikan dari suku mana orang tersebut.

Tinjau kembali bahasan dua buah proposisi majemuk yang ekivalen secara logika. Kita hanya juga dapat menggunakan definisi bikondisional untuk menyatakan keekivalenan. Ingatlah bahwa bikondisional bernilai benar jika dua proposisi otomiknya mempunyai nilai kebenaran sama. Oleh karena itu, bila dua proposisi majemuk yang ekivalen di bikondisionalkan, maka hasilnya adalah tautologi. Hal ini kita nyatakan pada definisi 1.8 berikut ini.

DEFINISI 1.8. Dua buah proposisi majemuk, P(p,q,…)   dan Q(p,q,…) disebut ekivalen secara logika, dilambangkan dengan P(p,q,…)   Q(p,q,…), jika P↔Q adalah tautologi.

Definisi 1.8 di atas mudah dimengerti. Dari tabel kebenaran bikondisional pada tabel 1.12 kita melihat bahwa bikondisonal hanya benar jika kedua proposisi mempunyai nilai kebenaran yang sama. Jika dua proposisi majemuk mempunyai tabel kebenaran yang sama, maka bikondisional terhadap kedua proposisi majemuk tersebut menghasilkan nilai yang semuanya benar, dengan kata lain tautologi.

Contoh 1.23

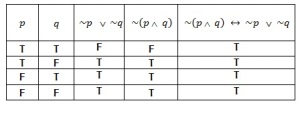
Tinjau kembali contoh 1.9 kita sudah membuktikan bahwa ~(p Λ q) ⇔  ~p v ~q. keekivalenan ini dapat juga kita tunjukkan dengan membikondisionalkan masing0masing proposisi majemuk tersebut. Dari tabel 1.14 terlihat bahwa ~(p Λ q) ↔ ~p v ~q. tautologi, dengan kata lain ~(p Λq)  ⇔ ~p v ~q.

Tabel 1.14 ~(p Λ q) ⇔  ~p v ~q adalah tautologi

4. Inferensi

Misalkan kepada kita diberikan beberapa proposisi. Kita dapat menarik kesimpulan baru dari deret proposisi tersebut. Proses penarikan kesimpulan penarkan kesimpulan dari beberapa proposisi disebut inferensi (inference).

Di dalam kalkulus proposisi, terdapat sejumlah kaidah inferensi, beberapa diantaranya adalah sebagai berikut :

1. Modus Ponen atau law of detachment

Kaidah ini didasarkan pada tautologi ((p Λ (p→q))→q, yang dalam hal ini, p dan p→q adalah hipotesis, sedangkan q adalah konklusi. Kaidah modus ponen dapat ditulis dengan cara :

Simpol ∴ dibaca sebagai “jadi” atau “karena itu”. Modus Ponen menyatakan bahwa jika hipotesis p dan implikasi p→q benar, maka konklusi q benar.

Contoh 1.24

Misalkan implikasi “ Jika 20 habis dibagi 2, maka 20 adalah bilangan genap” dan hipotesis “20 habis dibagi 2” keduanya benar. Maka menurut modus ponen, inferensi berikut :

“ Jika 20 habis dibagi 2, maka 20 adalah bilangan genap. 20 habis dibagi 2. Karena itu, 20 adalah bilangan genap”.

Adalah benar. Kita juga dapat menuliskan inferensi di atas sebagai :

Jika 20 habis dibagi 2, maka 20 adalah bilangan genap

20 habis dibagi 2

∴ 20 adalah bilangan genap

 

2. Modus Tollen

kaidah ini didasarkan pada tautologi [~q Λ(p→q)]→~p, Kaidah ini modus tollens ditulis dengan cara :

p→q

~q

∴~ p

 

Contoh 1.25

Misalkan implikasi “Jika n bilangan ganjil, maka n^2 bernilai ganjil” dan hipotesis “n^2 bernilai genap” keduanya benar. Maka menurut modus tollen inferensi berikut

Jika n bilangan ganjil, maka n^2 bernilai ganjil

n^2 bernilai genap

∴n bukan bilangan ganjil

Adalah benar.

 

3. Modus Hipotetis

Kaidah ini didasarkan pada tautologi [(p→q)Λ(q→r)]→(p→r). kaidah silogisme ditulis dengan cara :

p→q

q→r

∴p→r

Contoh 1.26

Misalkan imlikasi “Jika saya belajar dengan giat,, maka saya lulus ujian” dan implikasi “Jika saya lulus ujian, maka saya cepat menikah” adalah benar. Maka menurut kaidah silogisme, inferensi berikut :

Jika saya belajar dengan giat,, maka saya lulus ujian

Jika saya lulus ujian, maka saya cepat menikah

∴ Jika saya belajar dengan giat maka saya cepat menikah

Adalah benar

 

4. Silogisme Disjungtif

Kaidah ini didasarkan pada tautologi [(p v q) Λ~p]→q. Kaidah silogisme disjungtif ditulis dengan cara :

p v q

~p

∴ q

Inferensi berikut :

“ Saya belajar dengan giat atau saya menikah tahun depan.

Saya tidak belajar dengan giat. Karena itu, saya menikah tahun depan”.

Menggunakan kaidah silogisme disjungtif, atau dapat ditulis dengan cara :

Saya belajar dengan giat atau saya menikah tahun depan

Saya tidak belajar dengan giat. Karena itu, saya menikah tahun depan

∴ saya menikah tahun depan.

 

5. Simplifikasi

Kaidah ini didasarkan pada tautologi (pΛ q)→q, yang dalam hal ini, p dan q adalah hipotesis, sedangkan p adalah konklusi. Kaidah simpliikasi ditulusi dengan cara :

pΛ q

∴ p

Contoh 1.28

penarikan kesimpulan seperti berikut ini :

“ Hamid adalah mahasiswa ITB dan mahasiswa Unpar. Karena itu, Hamid adalah mahasiswa ITB”

Menggunakan kaidah simplifikasi, atau dapat juga ditulis dengan cara :

Hamid adalah mahasiswa ITB dan mahasiswa Unpar

∴Hamid adalah mahasiswa ITB.

Simplifikasi berikut juga benar.

“ Hamid adalah mahasiswa ITB dan mahasiswa Unpar. Karena itu, Hamid adalah mahasiswa Unpar”

Karena urutan proposisi di dalam konjungsi p qtidak mempunyai pengaruh apa-apa.

 

6. Penjumlahan

Kaidah ini didasarkan pada tautologi p→(p v q). Kaidah penjumlahan ditulis dengan cara

p

∴ p v q

Contoh 1.29

Penarikan kesimpulan seperti berikut ini :

“Taslim mengambil kuliah Matematika Diskrit. Karena itu, taslim mengambil kuliah Matematika Diskrit atau mengulang kuliah Algoritma”.

Menggunakan kaidah penjumlahan, atau dapat juga ditulis dengan cara :

Taslim mengambil kuliah Matematika Diskrit

∴ Taslim mengambil kuliah Diskrit atau mengulang kuliah Algoritma

 

7. Konjungsi

Kaidah ini didasarkan pada tautologi ((p)Λ (q) ) →(p Λ q). Kaidah konjungsi ditulis dengan cara :

 

p

q

∴ p Λ q

Contoh 1.30

Penarikan kesimpulan seperti berikut ini :

“Taslim mengambil kuliah Matematika Diskrit. Taslim mengulang kuliah Algoritma. Karena itu, taslim mengambil kuliah Matematika Diskrit dan mengulang kuliah Algoritma”.

Menggunakan kaidah konjungsi, atau dapat juga ditulis dengan cara :

Taslim mengambil kuliah Matematika Diskrit

Taslim mengulang kuliah Algoritma

∴ Taslim mengambil kuliah Diskrit dan mengulang kuliah Algoritma